3.2 — Marginal Productivity Theory
ECON 452 • History of Economic Thought • Fall 2020
Ryan Safner
Assistant Professor of Economics
safner@hood.edu
ryansafner/thoughtF20
thoughtF20.classes.ryansafner.com
Second-Generation Marginalists

Primarily extended and applied Jevons, Menger, & Walras’ marginalist tendencies to more problems in economics
- especially, the problem of pricing the factors of production
In England: Alfred Marshall, Phillip Wicksteed, Francis Edgeworth, A.C. Pigou
In Austria: Friedrich Wieser, Eugen von Böhm-Bawerk
In Switz./Italy: Enrico Barone, Vilfredo Pareto
In United States: John Bates Clark, Irving Fisher, Frank Knight, Frank Fetter
In Sweden: Knut Wicksell
Second-Generation Austrian Marginalists
Friedrich von Wieser

Friedrich von Wieser
1851—1926
Student of Menger, ultimately replaced Menger as Professor of Political Economy at University of Vienna
Coined the term “marginal utility” (Grenznutzen)
Teacher to F.A. Hayek
1889, Der natürliche Werth (Natural Value)
1914, Theorie der gesellschaftlichen Wirtschaft (Theory of Social Economy),
Friedrich von Wieser: Alternative Cost Theory

Friedrich von Wieser
1851—1926
What role do costs of production (payments to factors) play in value of final goods?
Costs are the values which are forgone in directing resources to a particular production process rather than other production processes
In this sense, production costs are really a reflection of utilities elsewhere in the economy
Alternative cost theory or opportunity cost
Friedrich von Wieser: Alternative Cost Theory

Friedrich von Wieser
1851—1926
Beginnings of major disagreements:
Jevons always thought costs were “real” in some sense, e.g. the disutility or pain of labor
- utility of consumption vs. disutility of production; utility & disutility curves
Marshall & Edgeworth would later argue you can derive an upward-sloping supply/cost curve for non-land factors by disutility of use
Friedrich von Wieser: Imputation Theory

Friedrich von Wieser
1851—1926
Menger had clear insights about capital and production: goods of higher order, their complementarity and substitutability, etc.
If we all agree that prices of final goods reflect their marginal utility, how do we price factor services (land, labor, capital)?
Wieser, using a legal term, this is a “problem of imputation”
Friedrich von Wieser: Imputation Theory

Friedrich von Wieser
1851—1926
Wieser’s solution was linear programming with simultaneous equations (no calculus)
Example: consider a three-good society, factors in each good’s production are x, y, and z, represented by three simultaneous equations:
x+y=1002x+3z=2904y+5z=590
Solve for x, y, and z (prices of each factor)
Assumes prices for final goods are given, fixed production coefficients, and no substitution of factors
Wieser, Friedrich von, 1893, Natural Value p.88
Eugen von Böhm-Bawerk

Eugen von Böhm-Bawerk
1851—1914
Studied law at University of Vienna; exposed to Menger but never his direct student
Friend & brother-in-law to Friedrich Wieser
Became Minister of Finance of Austria-Hungary; amabassador to Germany
Later became professor of political economy, teacher to Ludwig von Mises
Eugen von Böhm-Bawerk

Eugen von Böhm-Bawerk
1851—1914
Direct critique of Marxism: 1896, Karl Marx and the Close of His System
Famously wrote on capital theory and interest theory
- We will dig into this next week
Capital & Interest 2 volumes:
- 1884, History and Critique of Interest Theories
- 1889, Positive Theory of Capital
Eugen von Böhm-Bawerk

Eugen von Böhm-Bawerk
1851—1914
Took a different approach to the imputation problem (factor pricing) than Wieser:
Followed a phrase in Menger, “the loss principle” — applying to the price of the final good what would be lost if one of the factor services is withdrawn
A good start, but in truth, marginal product operates at infinitesimally small changes (derivative)
Eugen von Böhm-Bawerk: On Opportunity Cost

Eugen von Böhm-Bawerk
1851—1914
“If in any branch of production the price sinks below the cost...men will withdraw from that branch and engage in some better paying branch of production. Conversely, if in one branch of production, the market price of the finished good is considerably higher than the value of the sacrificed or expended means of production, then will men be drawn from less profitable industries. They will press into the better paying branch of production, until through the increased supply, the price is again forced down to cost.
Böhm-Bawerk, Eugen von, 1884, Capital and Interest
Eugen von Böhm-Bawerk: On Opportunity Cost

Eugen von Böhm-Bawerk
1851—1914
“What determine the amount of this cost? The amount of the cost is identical with the value of the productive power, and, as a rule, is determined by the money marginal utility of this productive power...The price of a definite specie of freely reproducible goods fixes itself in the long run at that point where the money marginal utility, for those who desire to purchase these products, intersects the money marginal utility of all those who desire to purchase in the other communicating branches of production. The figure of the two blade of a pair of shears still holds good. One of the two blade, whose coming together determine the height of the price of any species of product, is in truth the marginal utility of this particular product. The other, which we are wont to call "cost," is the marginal utility of the products of other communicating branches of production. Or, according to Wieser, the marginal utility of "production related goods." It is, therefore, utility and not disutility which, as well on the side of supply as of demand, determine the height of the price. This, too, even where the so-called law of cost plays its role in giving value to goods. Jevons, therefore, did not exaggerate the importance of the one side, but came very near the truth when he said "value depends entirely upon utility.” (45)
Price is Determined at the Margin: B-B’s Example

Böhm-Bawerk has a great demonstration of how markets work to set the price at the margin
- Story of the three “marginal pairs”
Imagine a small public horse market:
3 people, A, B, and C each own 1 horse
3 people, D, E, and F each are potentially interested in buying a horse
Based on Eugen von Böhm-Bawerk’s example in Capital and Interest (1884)
Price is Determined at the Margin: B-B’s Example
| Person | Reservation Price |
|---|---|
| Seller A | Minimum WTA: $400 |
| Seller B | Minimum WTA: $500 |
| Seller C | Minimum WTA: $600 |
| Buyer D | Maximum WTP: $600 |
| Buyer E | Maximum WTP: $500 |
| Buyer F | Maximum WTP: $400 |
Price is Determined at the Margin: B-B’s Example
| Person | Reservation Price |
|---|---|
| Seller A | Minimum WTA: $400 |
| Seller B | Minimum WTA: $500 |
| Seller C | Minimum WTA: $600 |
| Buyer D | Maximum WTP: $600 |
| Buyer E | Maximum WTP: $500 |
| Buyer F | Maximum WTP: $400 |
Suppose Buyer F announces she will pay $400 for a horse
Only Seller A is willing to sell at $400
Buyers D, E, and F are willing to buy at $400
- D and E are willing to pay more than F to obtain the 1 horse
- They raise their bids above $400 to attract sellers
Price is Determined at the Margin: B-B’s Example
| Person | Reservation Price |
|---|---|
| Seller A | Minimum WTA: $400 |
| Seller B | Minimum WTA: $500 |
| Seller C | Minimum WTA: $600 |
| Buyer D | Maximum WTP: $600 |
| Buyer E | Maximum WTP: $500 |
| Buyer F | Maximum WTP: $400 |
Suppose Seller C announces he will sell his horse for $600
Only Buyer D is willing to buy at $600
Sellers A, B, and C are willing to sell at $600
- A and B are willing to accept less than C to sell their horses
- They lower their asks below $600 to attract buyers
Price is Determined at the Margin: B-B’s Example
| Person | Reservation Price |
|---|---|
| Seller A | Minimum WTA: $400 |
| Seller B | Minimum WTA: $500 |
| Seller C | Minimum WTA: $600 |
| Buyer D | Maximum WTP: $600 |
| Buyer E | Maximum WTP: $500 |
| Buyer F | Maximum WTP: $400 |
Market Price: $500
If the market price reaches $500 (through bids and asks changing)
Sellers A and B sell their horses for $500 each
- Buyers D and E buy them at $500 each
Price is Determined at the Margin: B-B’s Example
| Person | Reservation Price |
|---|---|
| Seller A | Minimum WTA: $400 |
| Seller B | Minimum WTA: $500 |
| Seller C | Minimum WTA: $600 |
| Buyer D | Maximum WTP: $600 |
| Buyer E | Maximum WTP: $500 |
| Buyer F | Maximum WTP: $400 |
Market Price: $500
At $500, B and E are the "marginal" buyer and seller, the "last" ones that just got off the fence to exchange in the market
- B has WTA just low enough to sell
- E has WTP just high enough to buy
The marginal pair actually are the ones that "set" the market price!
Price is Determined at the Margin: B-B’s Example
| Person | Reservation Price |
|---|---|
| Seller A | Minimum WTA: $400 |
| Seller B | Minimum WTA: $500 |
| Seller C | Minimum WTA: $600 |
| Buyer D | Maximum WTP: $600 |
| Buyer E | Maximum WTP: $500 |
| Buyer F | Maximum WTP: $400 |
Market Price: $500
Notice the most possible exchanges take place at a market price of $500
- 2 horses get exchanged
Any price above or below $500, only 1 horse would get exchanged
- Also, at least one other buyer or seller would raise/lower their bid/ask
Price is Determined at the Margin: B-B’s Example
| Person | Reservation Price |
|---|---|
| Seller A | Minimum WTA: $400 |
| Seller B | Minimum WTA: $500 |
| Seller C | Minimum WTA: $600 |
| Buyer D | Maximum WTP: $600 |
| Buyer E | Maximum WTP: $500 |
| Buyer F | Maximum WTP: $400 |
Market Price: $500
- At $500, C and F are the "excluded" buyers and sellers
- C has WTA too high to sell
- F has WTP too low to buy
Price is Determined at the Margin: B-B’s Example
| Person | Reservation Price |
|---|---|
| Seller A | Minimum WTA: $400 |
| Seller B | Minimum WTA: $500 |
| Seller C | Minimum WTA: $600 |
| Buyer D | Maximum WTP: $600 |
| Buyer E | Maximum WTP: $500 |
| Buyer F | Maximum WTP: $400 |
Market Price: $500
At $500, A and D are the "inframarginal" buyers and sellers
- A has WTA lower than market price, earns extra $100 surplus from exchange
- D has WTP higher than market price, earns extra $100 surplus from exchange
These buyers and sellers benefit the most from exchange
Marginal Productivity Theory
The Ricardian Roots of Marginal Productivity Theory

David Ricardo
1772-1823
Ricardo’s theory of rent applied marginal analysis (“doses” of L+K) to a fixed factor (land), concluding the fixed factor earns a residual surplus (gap between AP>MP) of variable factor (L+K)
Marginal productivity theory takes the other side of the coin: any variable factor must earn a payment equal to its marginal product (holding all other factors fixed)
Marginal Productivity Theory
Applying Ricardian logic beyond agriculture, we arrive at the modern law of diminishing returns
- “Law of variable proportions” or “variation of returns”
For any one variable factor (holding all others constant), increasing use will eventually yield a diminishing marginal product
- nothing special about land!
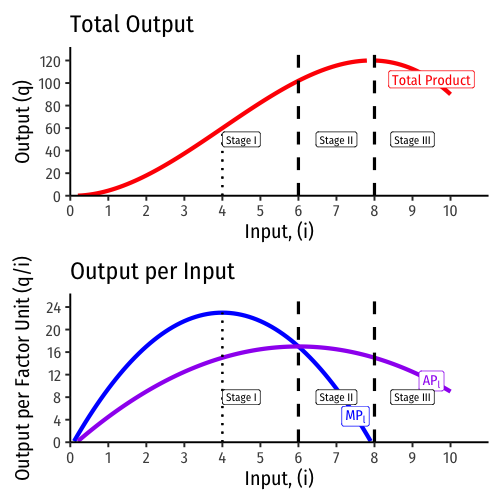
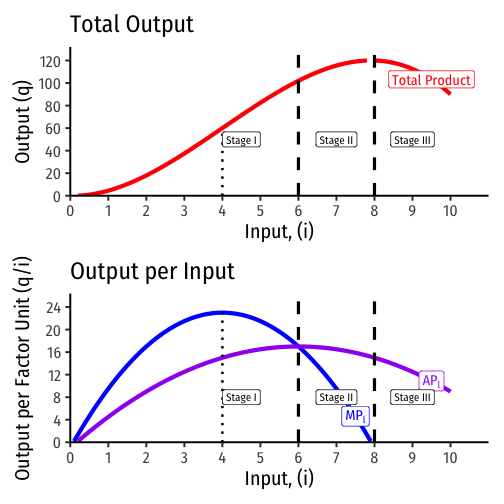
Diminishing Returns
Marginal product of factor i, (MPi): additional output produced by adding one more unit of factor i (holding all others constant) MPi=ΔqΔi
- MPi is slope of TP at each value of i
Average product of factor i (APi): additional output produced by adding one more unit of factor i (holding all others constant) APi=qi
- APi is slope of a ray from the origin to the production function at any quantity of i
Derived Demand in Factor Markets
Demand for factors (e.g. labor) is a “derived demand”:
- Firm only demands inputs to the extent they contribute to producing sellable output
Firm faces a tradeoff when hiring more labor, as more labor ΔL creates:
- Marginal Benefit: Increases output and thus revenue
- Marginal Cost: Increases costs

Marginal Revenue Product (of Labor)
- Hiring more labor increases output (i.e. labor's MPL)
- Recall: MPL=ΔqΔL, where q is units of output
Marginal Revenue Product (of Labor)
Hiring more labor increases output (i.e. labor's MPL)
- Recall: MPL=ΔqΔL, where q is units of output
Additional output generates (i.e. labor's MR(q))
- Recall: MR(q)=ΔR(q)Δq, where R(q) is total revenue
Marginal Revenue Product (of Labor)
Hiring more labor increases output (i.e. labor's MPL)
- Recall: MPL=ΔqΔL, where q is units of output
Additional output generates (i.e. labor's MR(q))
- Recall: MR(q)=ΔR(q)Δq, where R(q) is total revenue
- Hiring more labor, on the margin, generates a benefit, called the marginal revenue product of labor, MRPL:
MRPL=MPL∗MR(q)
- i.e. the number of new products a new worker makes times the revenue earned by selling the new products
Marginal Revenue Product for Competitive Firms
- This is the Firm's Demand for Labor:
MRPL=MPL∗MR(q)
- For a firm in a competitive (output) market, firm's MR(q)=p, hence:
MRPL=MPL∗p
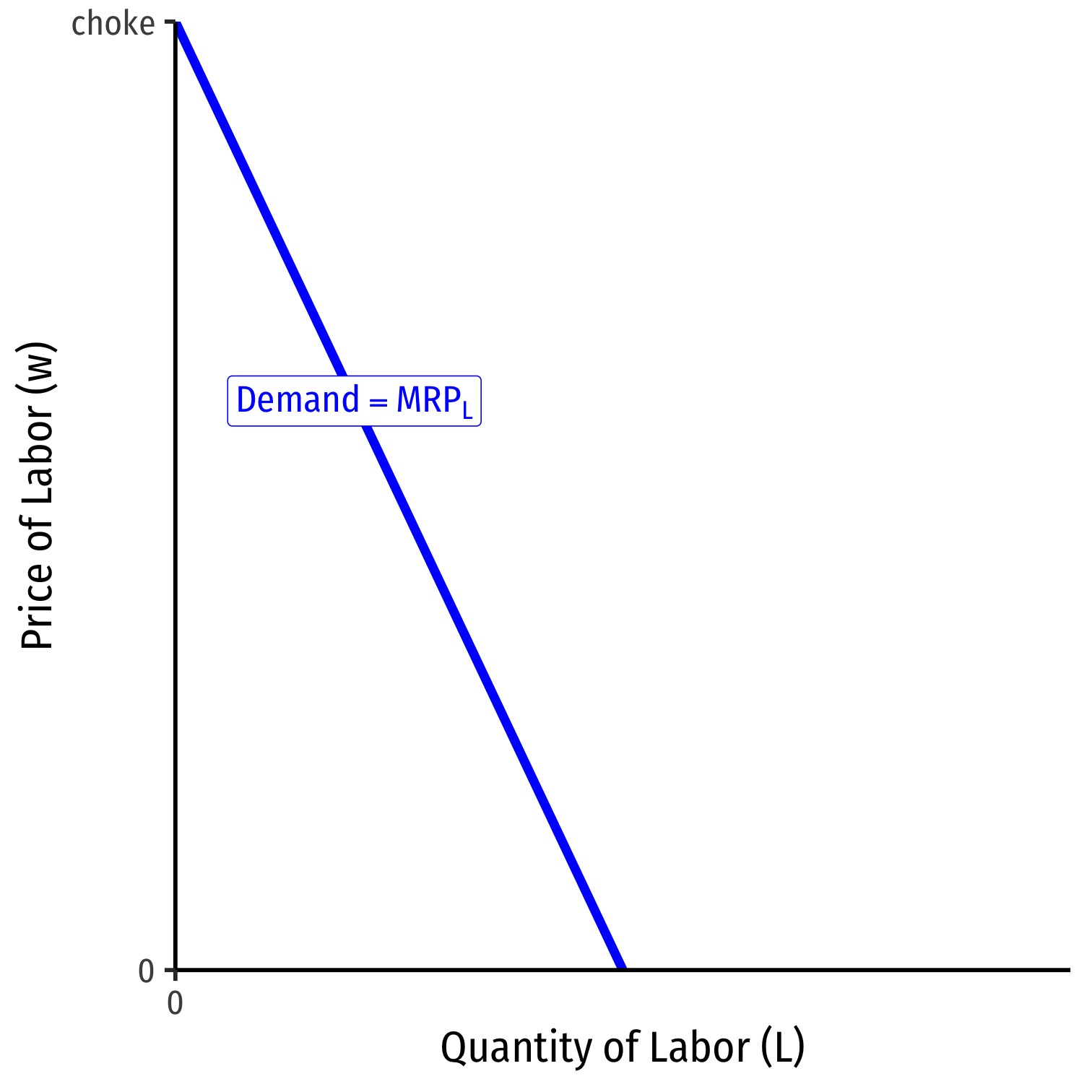
Marginal Revenue Product for Competitive Firms
MRPL=MPL∗p
Marginal benefit of hiring labor, MRPL falls with more labor used
- production exhibits diminishing marginal returns to labor!
Choke price for labor demand: price too high for firm to purchase any labor
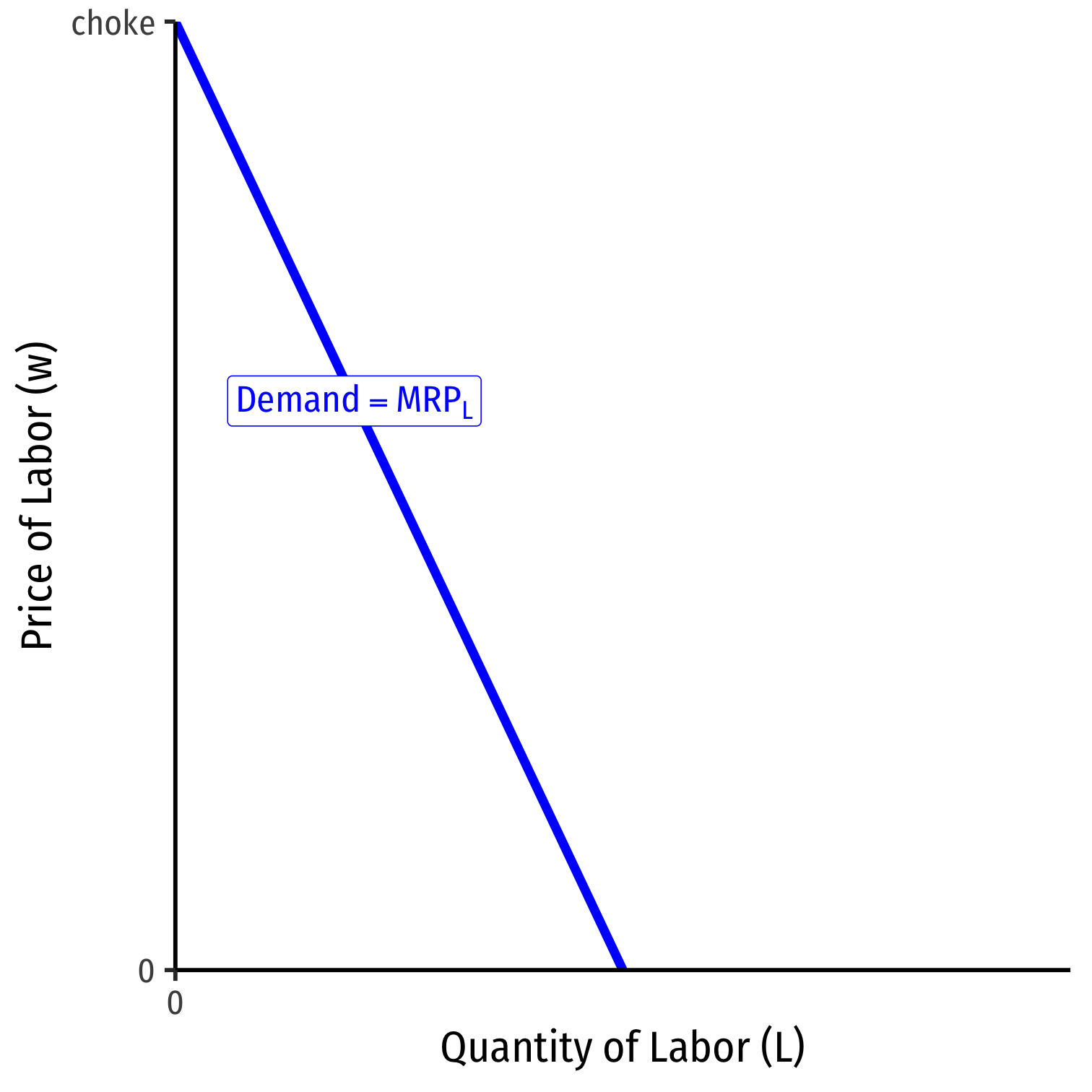
A Competitive Factor Market
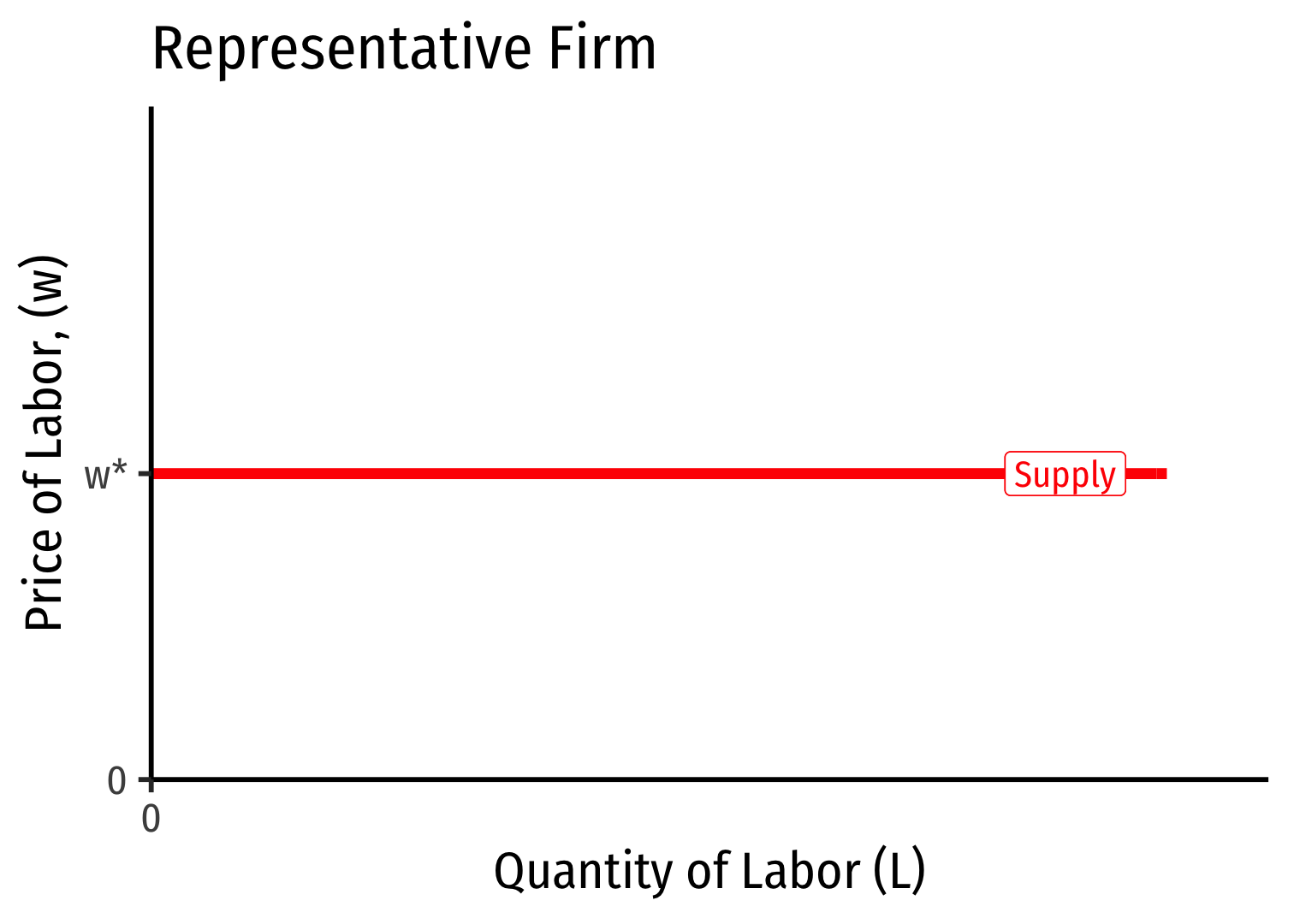
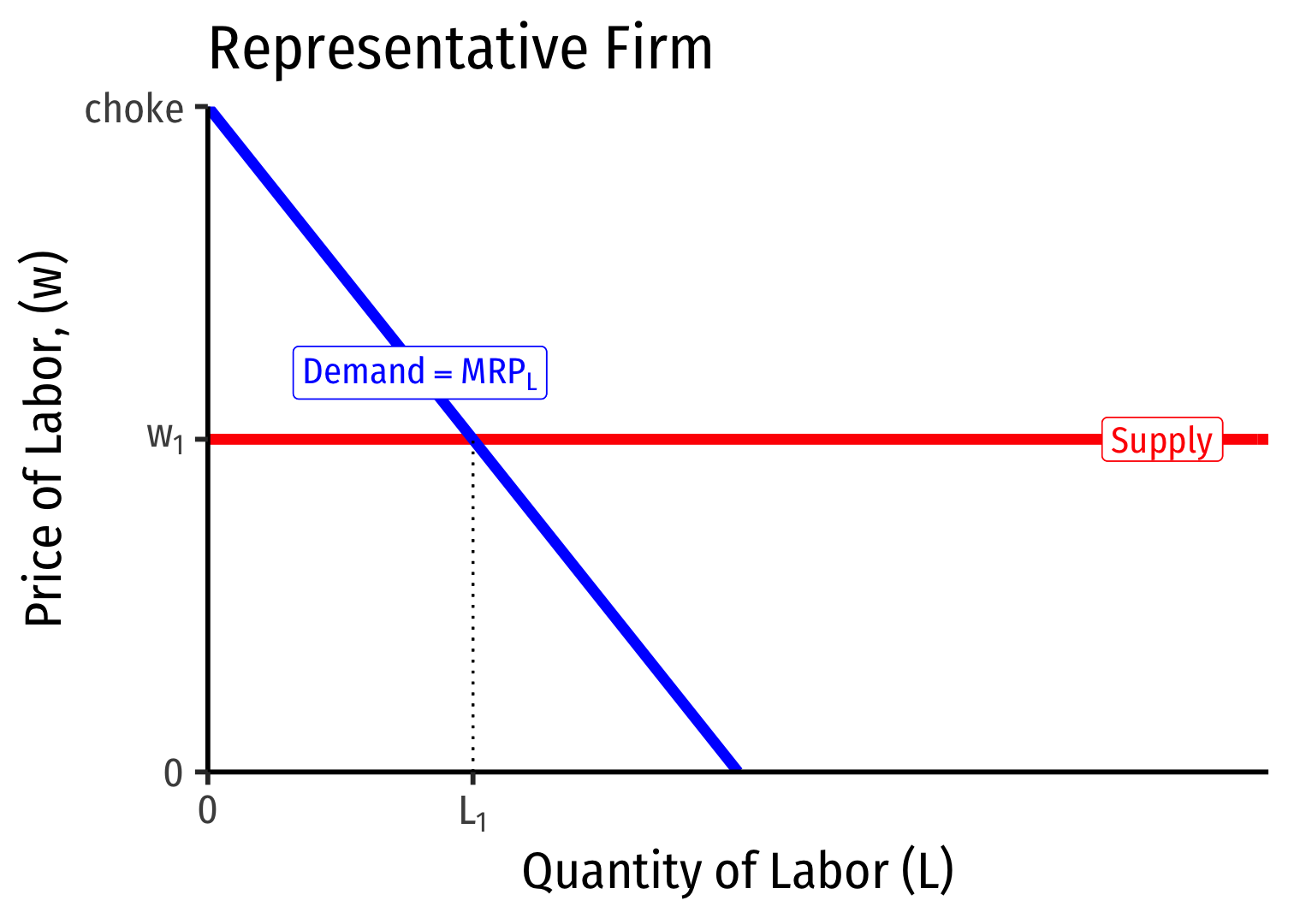
- If the factor market is competitive, labor supply for an individual firm is perfectly elastic at the market price of labor (w∗)
Labor Supply and Firm's Demand for Labor
We've seen a falling MRPL, the marginal benefit of hiring labor
Marginal cost of hiring labor, w, remains constant
- so long as firm is not a big purchaser (has no market power) in the labor market
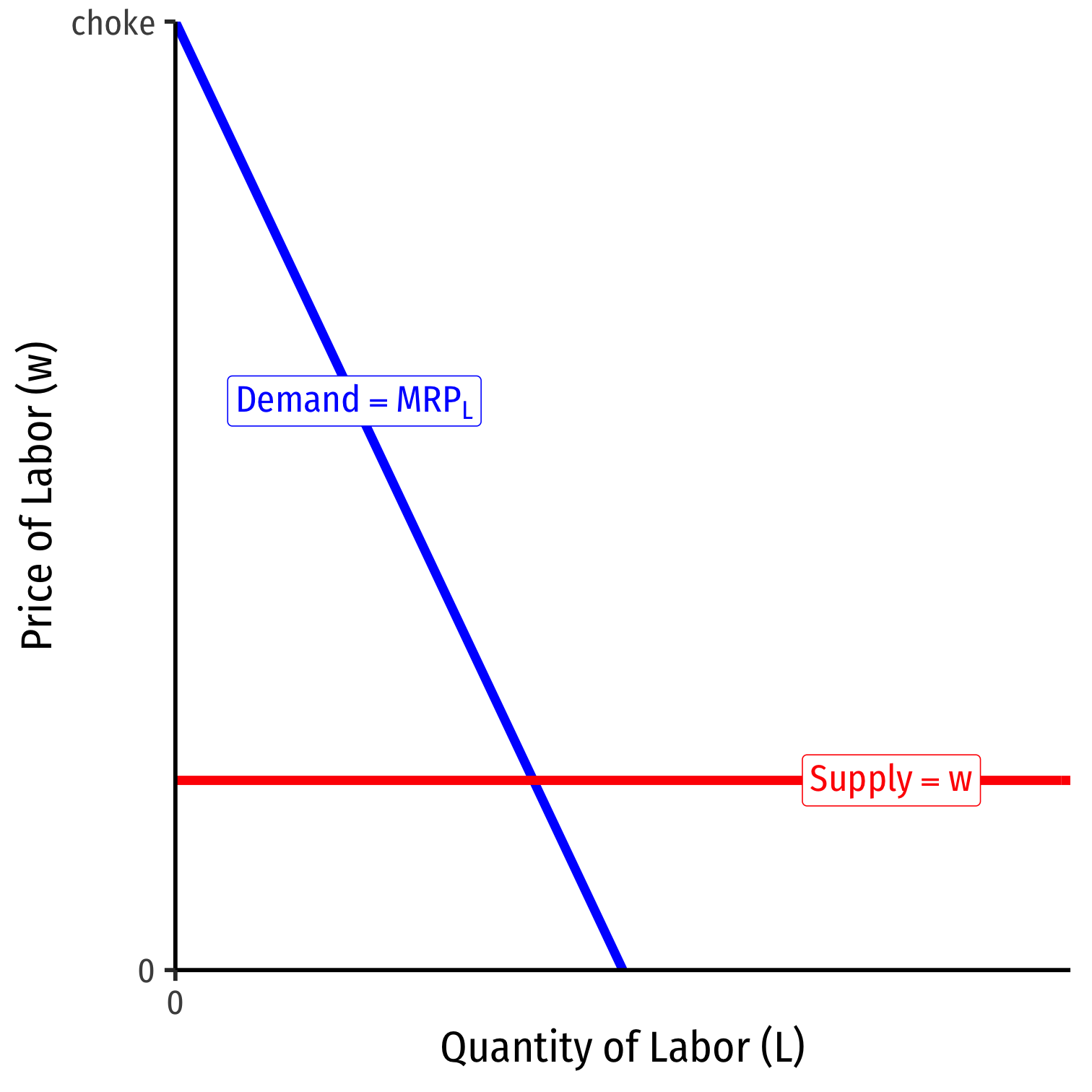
Labor Supply and Firm's Demand for Labor
At low amounts of labor, marginal benefit (MRPL)>w marginal cost
Firm will hire more labor
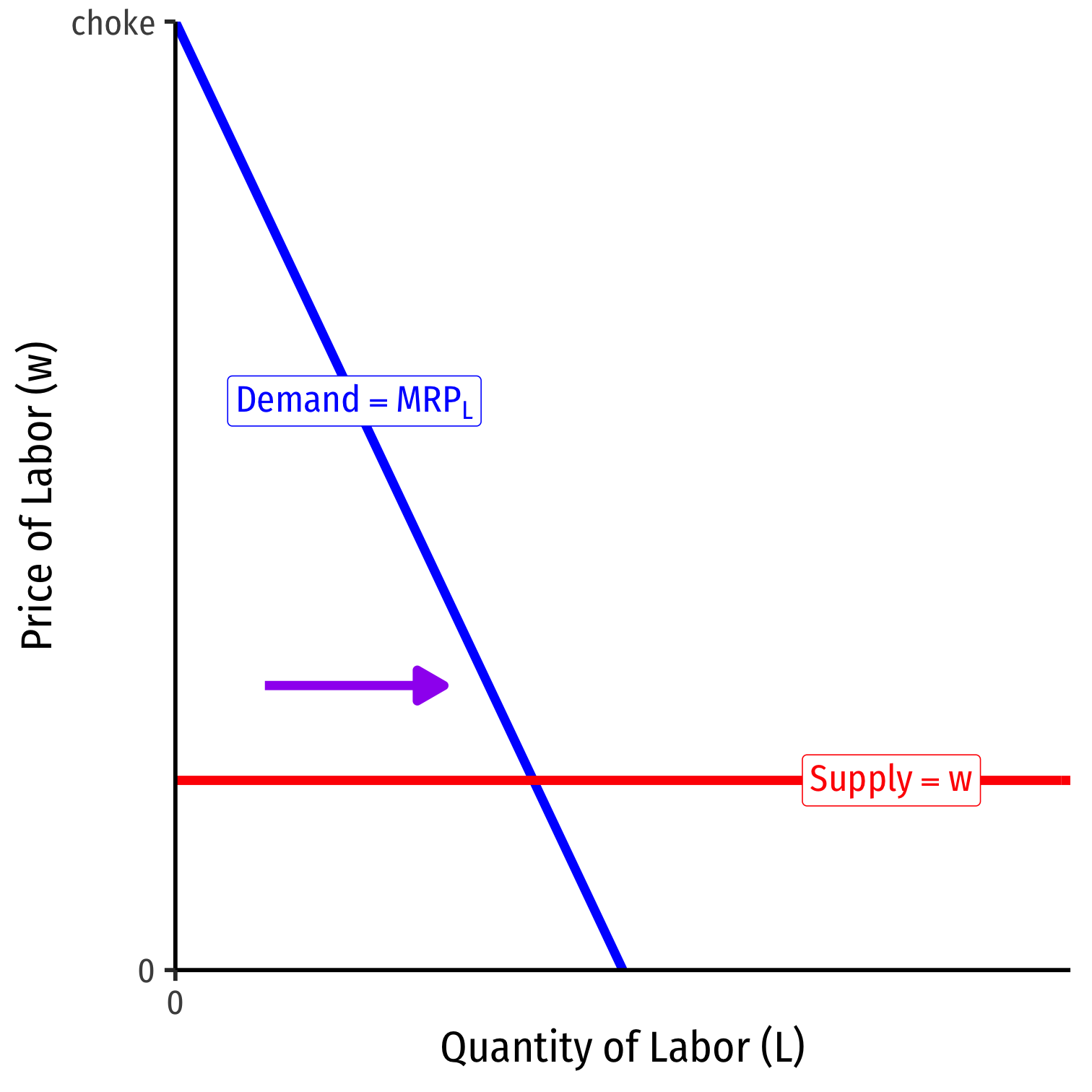
Labor Supply and Firm's Demand for Labor
At high amounts of labor, marginal benefit (MRPL)<w marginal cost
Firm will hire less labor
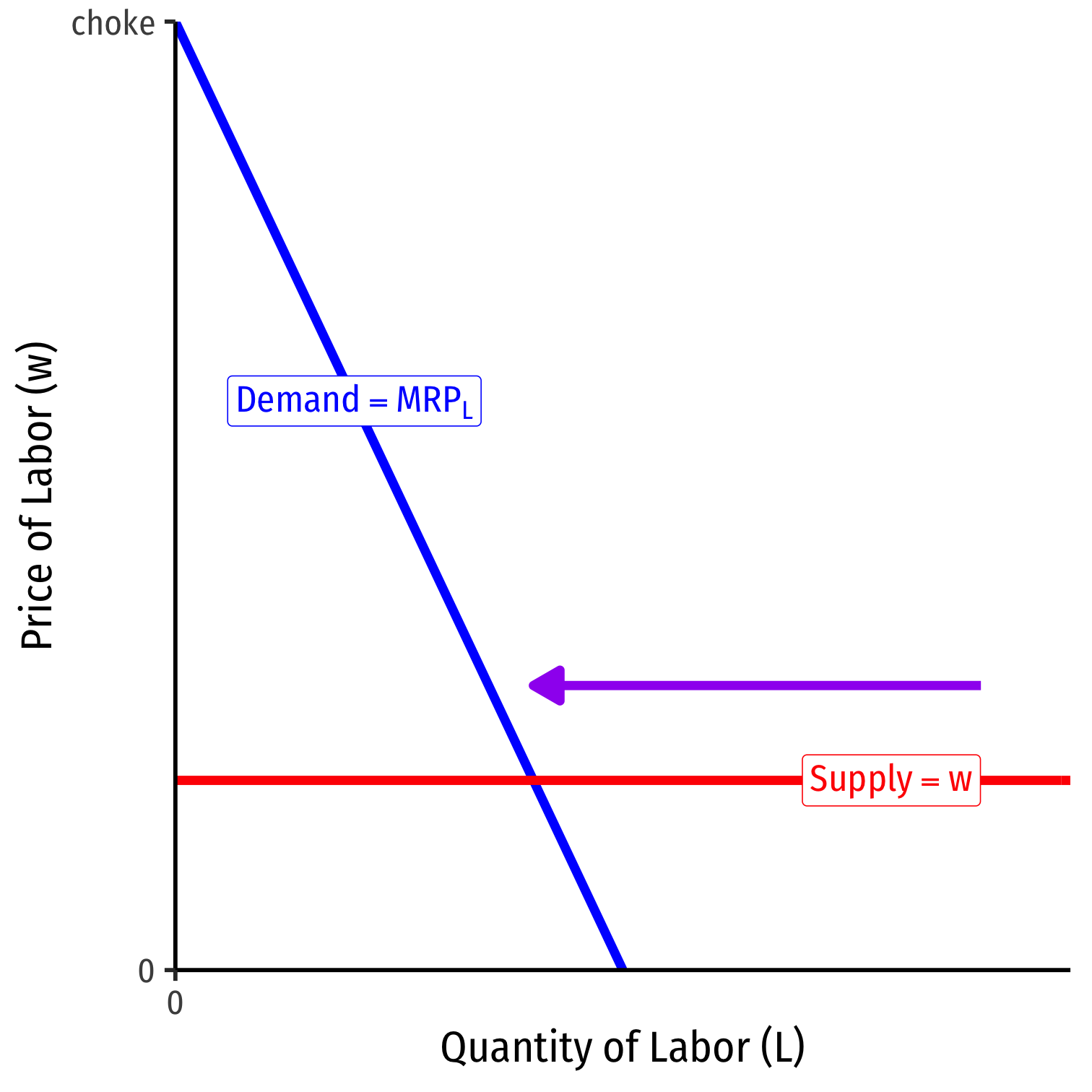
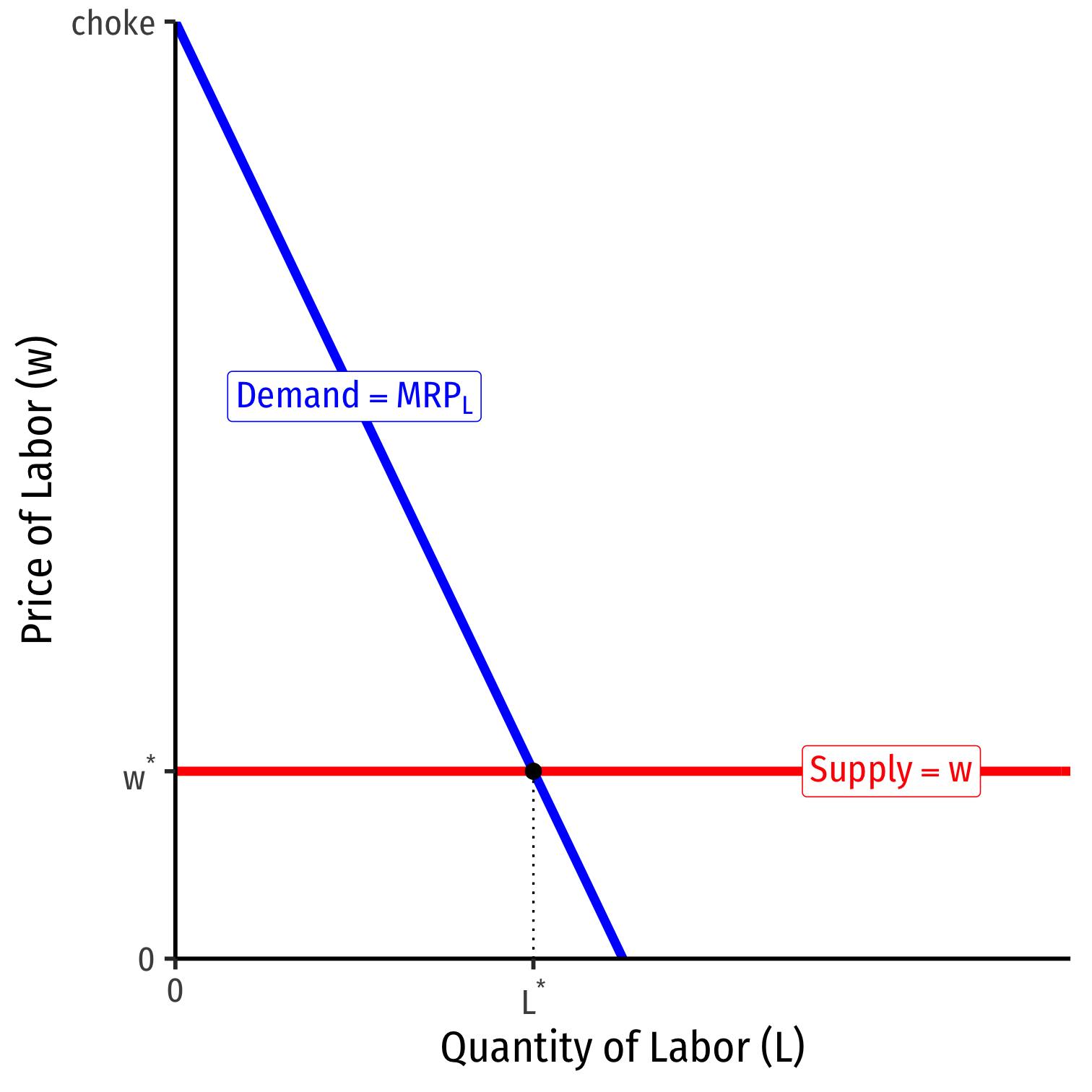
Labor Supply and Firm's Demand for Labor
Firm hires L∗ optimal amount of labor where w=MRPL
i.e. marginal cost of labor = marginal benefit of labor
Labor Supply and Firm's Demand for Labor
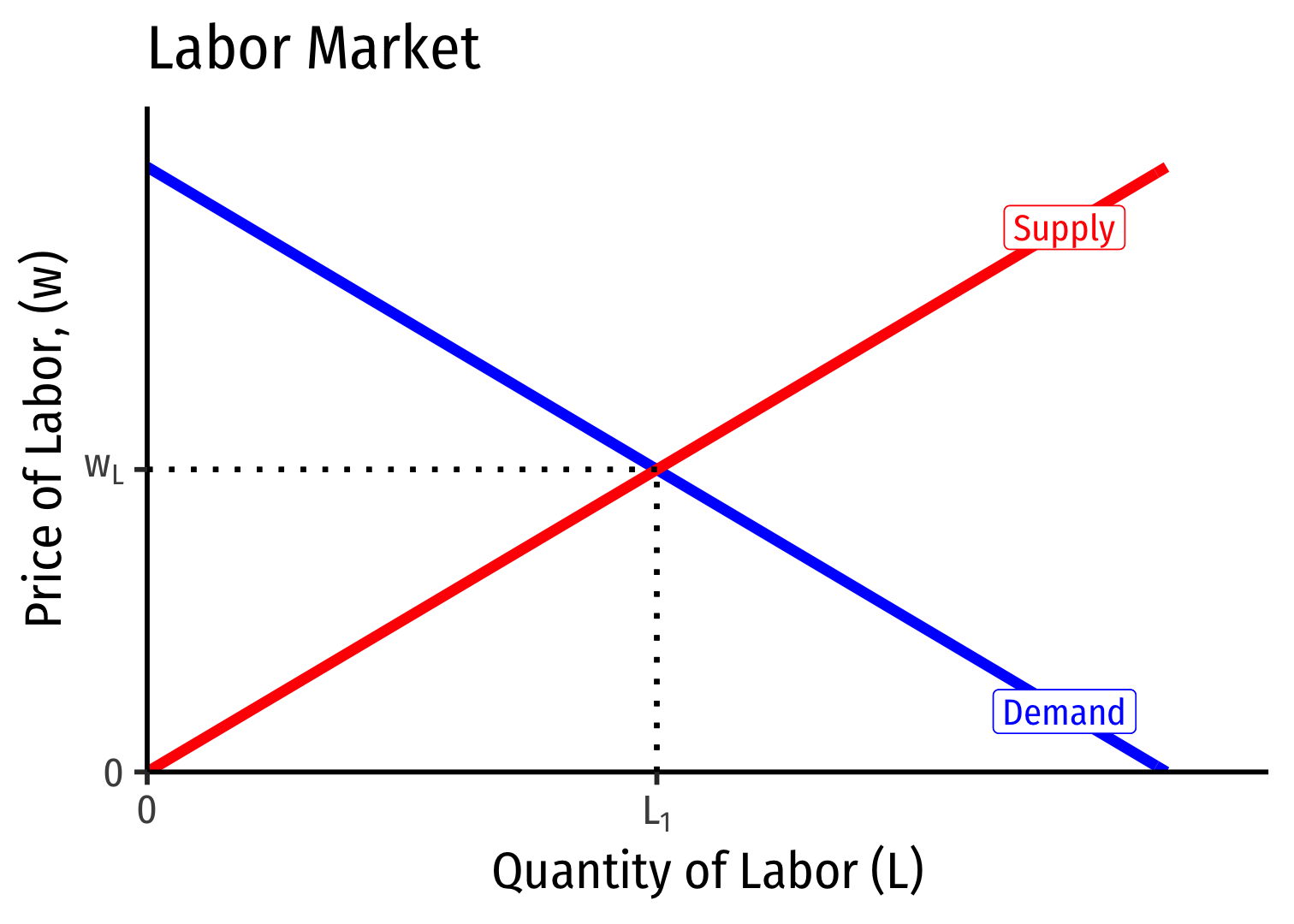
Labor Supply and Firm's Demand for Labor
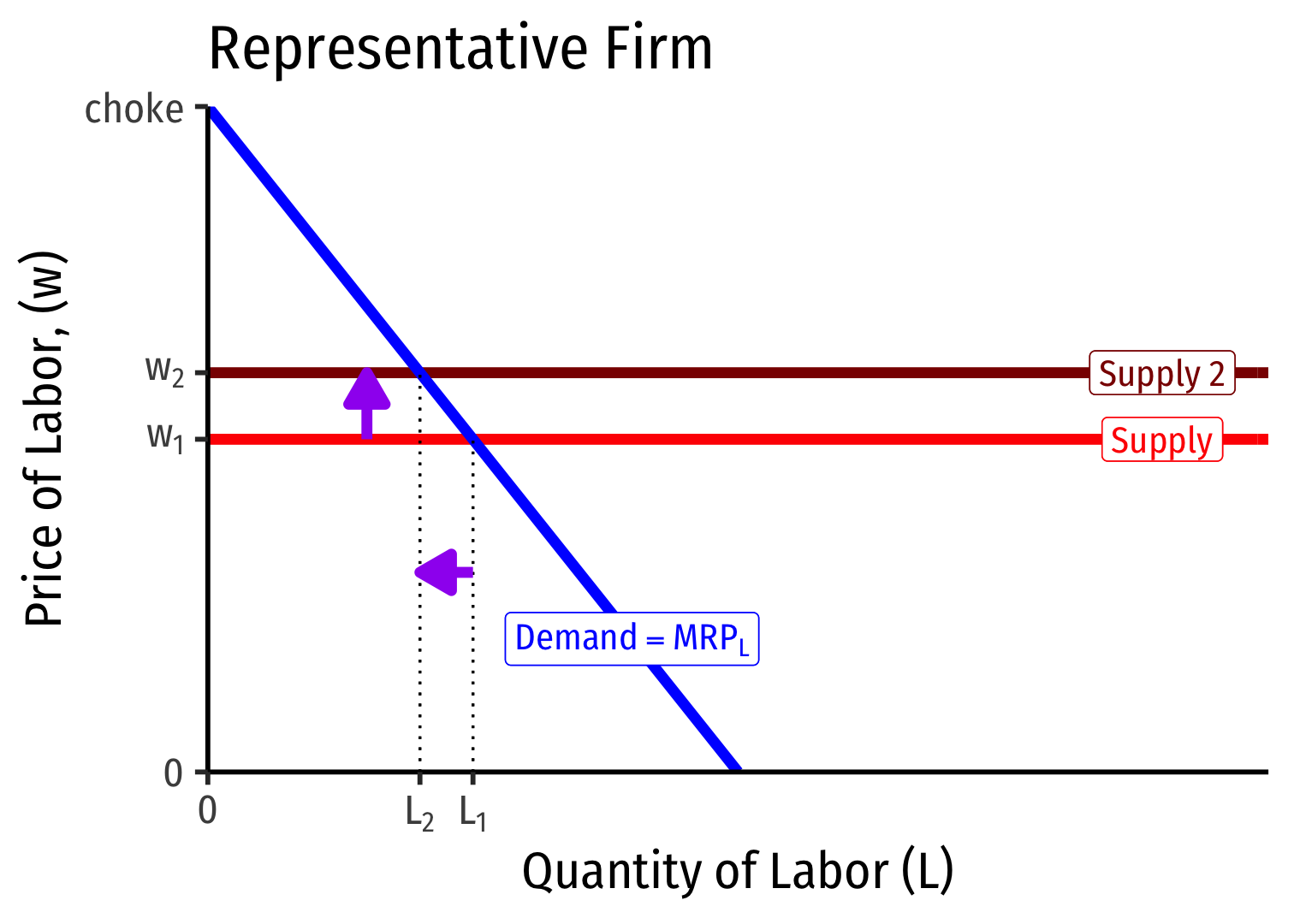
- If market supply of labor decreases, firms hire fewer workers, at higher wages (and vice versa)
Multiple Inputs and Cost Minimization
But firms produce with many factors, what is the more general rule for hiring the optimal combination of factors?
Assume three factors: land, labor, capital
Optimal hiring condition is the equimarginal rule (Gossen’s Second Law} again:
MPlpl=MPkpk=MPtpt=⋯=MPnpn
- Cost of production is minimized where the marginal product per dollar spent is equalized across all n possible inputs
- the “last dollar spent” on each input provides the same marginal product

Product Exhaustion & The Morality of Marginal Productivity
John Bates Clark

John Bates Clark
1847—1938
Initially a German Historicist (studied under Karl Knies) in Germany; a Christian socialist
Became professor at Columbia, independently derived his own version of marginal utility theory
Main popularizer of marginal productivity theory, virtues of market competition; opponent to American Institutionalists (see later)
1886, The Philosophy of Wealth
1889, “Possibility of a Scientific Law of Wages” paper at AEA; generalized in 1899 The Distribution of Wealth
Product Exhaustion
Ricardian rent theory defined rent as a residual, will always adjust to fill the gap between output price and wages & profits
- output price = wages & profits + rent
Thus, the payments to all factors of production (land, labor, capital) “fully exhaust the product”
- i.e. the sum of factor payments (costs to firm) equals the price
Product Exhaustion
On a competitive market, each product is paid its marginal (revenue) product
Does the sum of these marginal products exactly equal the market price of the output?
- “Product Exhaustion” debate:
Q=?MPL×L+MPK×K+MPT×T

John Bates Clark

John Bates Clark
1847—1938
Clark famously argued that on a competitive market, each factor is paid its marginal product, and that this exactly exhausts the product
Viewed this as a moral virtue of markets: each factor is paid for its contribution to society
- factor prices are not only efficient, they are just
Offered no proof that this is true
John Bates Clark: The Morality of Marginal Productivity

John Bates Clark
1847—1938
Meant this as a critique of both Karl Marx and Henry George
Georgists believed rent was undeserved, unearned income of landowners: should go to government
Marxists believed profit was exploitatibe and undeserved (surplus value): belonged to workers
Clark’s Distribution of Wealth argues that marginal productivity theory shows that under competitive markets, each factor is paid its just due
- Labor and land and capital are all necessary for production, and are paid for their productive contributions
John Bates Clark: The Morality of Marginal Productivity

John Bates Clark
1847—1938
Furthermore, argues that the distribution of income (under competitive markets) is just and deserved!
Heavily criticized for this normative theory
- Problems: not perfectly competitive, monopolies, labor unions, etc.
- His student, Thorstein Veblen reached the opposite conclusion!
Hume’s is-ought gap
Phillip Wicksteed

Phillip Wicksteed
1844—1927
A British economist and unitarian minister
Learned economics from Jevons, and got inspired to write about political economy after reading Henry George
1894, An Essay on the Co-Ordination of the Laws of Distribution
- tries to solve the product exhaustion problem of marginal productivity theory
1910, The Common Sense of Political Economy: Including a Study of the Human Basis of Economic Law
- one of the greatest books popularizing marginalism
Phillip Wicksteed

Phillip Wicksteed
1844—1927
Uses Euler’s Theorem of homogeneous functions to prove product exhaustion under specific conditions:
- production functions must be linearly homogenous (of degree 1)
- cnY=f(cnL,cnK,cnT) only for n=1
- we would say: “constant returns to scale”
Criticized for this by many (Edgeworth, Pareto, Wicksell, etc.)
- John Hicks: “Where Wicksteed went wrong was his assumption that he could argue from the shape of the curve at one particular point to the general shape of the curve.”
Returns to Scale
- The returns to scale of production refers to the change in output when all inputs are increased at the same rate
Returns to Scale
The returns to scale of production refers to the change in output when all inputs are increased at the same rate
Constant returns to scale: output increases at same proportionate rate as inputs increase
- e.g. if you double all inputs, output doubles
Returns to Scale
The returns to scale of production refers to the change in output when all inputs are increased at the same rate
Constant returns to scale: output increases at same proportionate rate as inputs increase
- e.g. if you double all inputs, output doubles
- Increasing returns to scale: output increases more than proportionately to the change in inputs
- e.g. if you double all inputs, output more than doubles
Returns to Scale
The returns to scale of production refers to the change in output when all inputs are increased at the same rate
Constant returns to scale: output increases at same proportionate rate as inputs increase
- e.g. if you double all inputs, output doubles
- Increasing returns to scale: output increases more than proportionately to the change in inputs
- e.g. if you double all inputs, output more than doubles
- Decreasing returns to scale: output increases less than proportionately to the change in inputs
- e.g. if you double all inputs, output less than doubles
Constant Returns to Scale
Constant returns to scale: doubling all inputs ⟹ double output f(cl,ck,ct)=cf(l,k,t)∀c>1
Constant economies of scale: average and marginal costs (are equal and) do not vary with output
Total revenues are completely exhausted by the payments to factors (costs to firm)
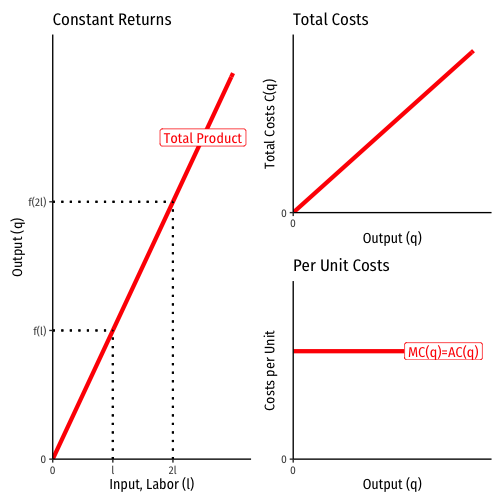
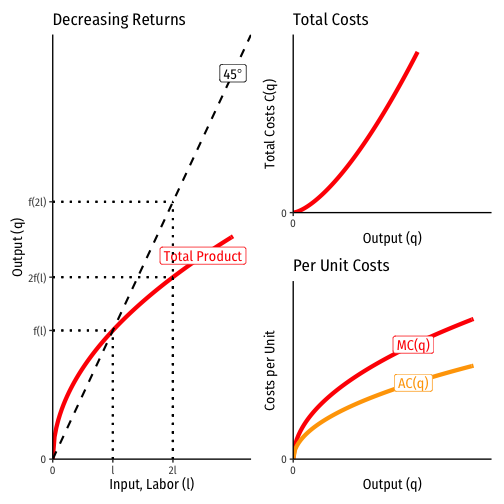
Decreasing Returns to Scale
Decreasing returns to scale: doubling all inputs ⟹ less than double output f(cl,ck,ct)<cf(l,k,t)∀c>1
Diseconomies of scale: average and marginal costs are increasing with output
- AC < MC ⟹ marginal cost pricing is always profitable
- Total Costs < Total Revenues ⟹π>0
Total revenues are not exhausted by the payments to factors (costs to firm); residual leftover!
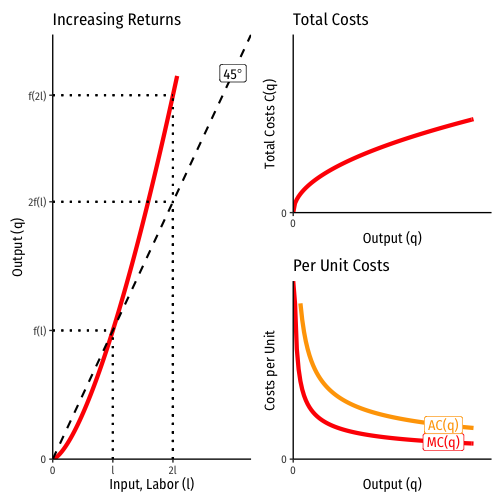
Increasing Returns to Scale
Increasing returns to scale: doubling all inputs ⟹ more than double output f(cl,ck,ct)>cf(l,k,t)∀c>1
Economies of scale: average and marginal costs are decreasing with output
- AC > MC ⟹ marginal cost pricing is always loss-inducing
- Total Costs > Total Revenues ⟹π<0
Total revenues are insufficient to cover the payments to factors (costs to firm); losses!
Knut Wicksell
Knut Wicksell
1851—1926
Swedish economist at University of Stockholm
Another supposed independent discoverer of marginal productivity theory
Made key contributions to capital and interest theory, influence Austrian & Keynesian schools of macroeconomics
- we'll explore more next week
1898, Interest and Prices
Wicksell and Product Exhaustion
Knut Wicksell
1851—1926
Most economists believed that an industry would always be either constant, increasing, or decreasing returns
Wicksell showed that most firms actually go through all three phases of returns to scale
- developing a long-run U-shaped average cost curve for a firm
- would take a few decades for neoclassical economists to derive and understand shape of AC curve
Wicksell and Product Exhaustion
Knut Wicksell
1851—1926
Thus, it is not necessary (as Wicksteed did) to assume constant returns to prove product exhaustion
Competition would ensure that in the long run, firms are producing at their least-cost combination
- p=MC=ACmin
- π=0
- “product exhaustion”
Wicksell and Product Exhaustion
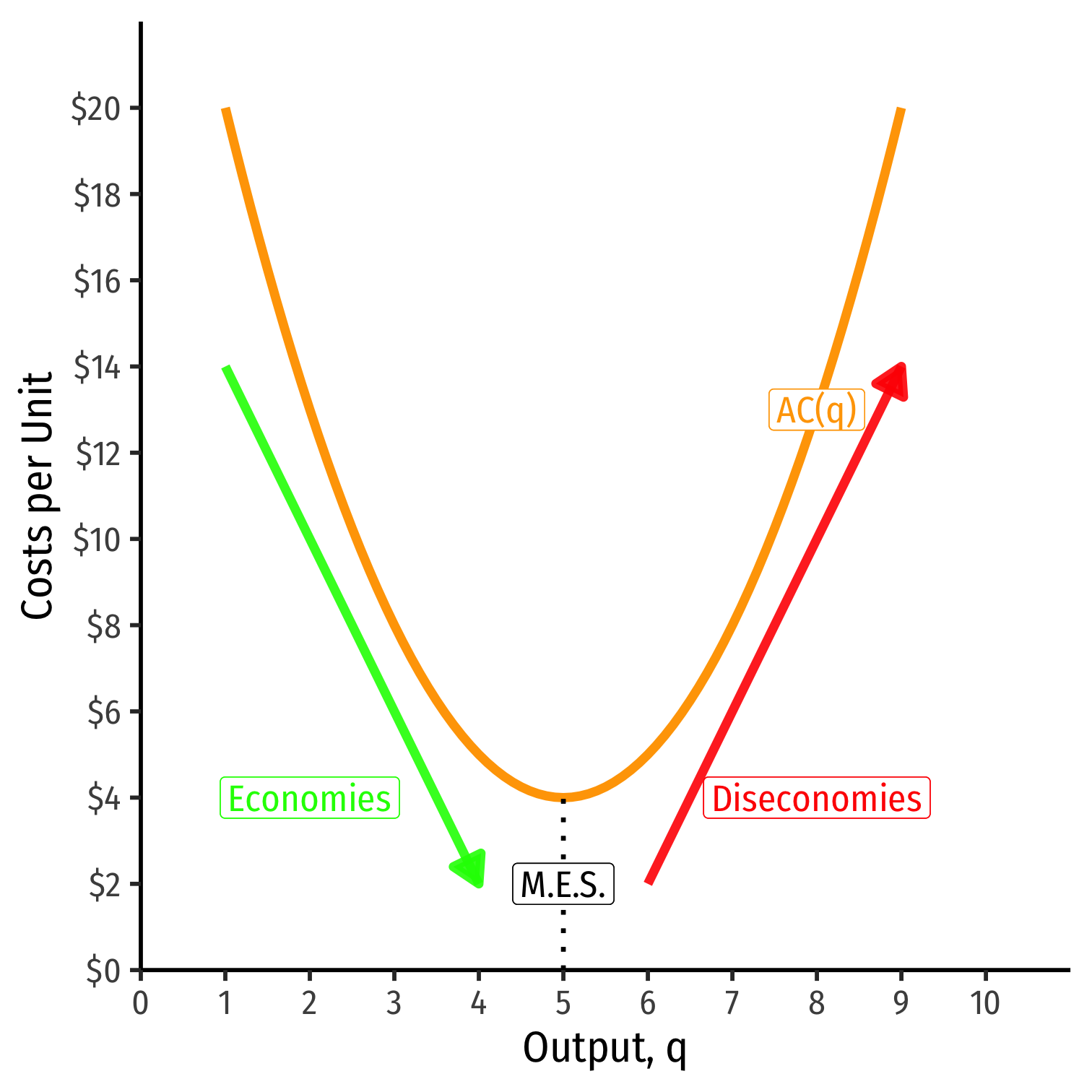
Minimum Efficient Scale: q with the lowest AC(q)
- constant returns to scale
Economies of Scale: ↑q, ↓AC(q)
- increasing returns to scale
Diseconomies of Scale: ↑q, ↑AC(q)
- decreasing returns to scale
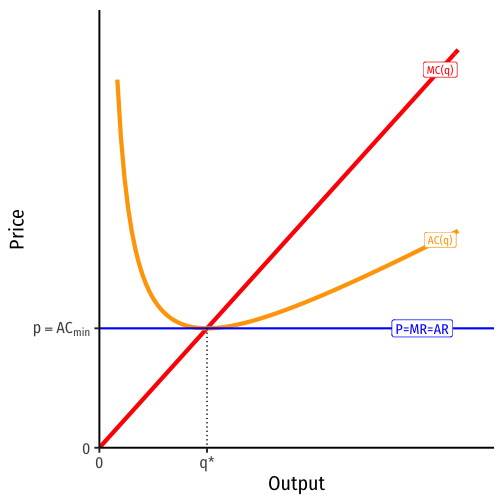
Wicksell and Product Exhaustion
Think about what you learn in microeconomics
In perfect competition, in the long run, as profits attract entrants and losses force exits, price settles on the break-even point, where profit is 0
- p=MC=ACmin
- factors are paid their opportunity costs (marginal products); nothing leftover
We still haven’t gotten to the famous model of perfect competition, but this is where everything is heading
Implications & Criticisms of Marginal Productivity Theory
Implications of Marginal Productivity Theory

John Bates Clark
1847—1938
Several flaws with marginal productivity theory as a theory of distribution
MPT is primarily a theory of factor pricing, not about distribution of relative shares
It’s even an incomplete theory of factor pricing!
- Considers only demand side of factor market (firms), not the supply side!
Assumes competitive output and input markets
- Labor unions, monopsony power, bargaining, etc.
Implications of Marginal Productivity Theory
- A big problem: it’s impossible to observe and measure an individual factor’s marginal product!
“there is no separate product of the tool on the one hand and of the labor using the tool on the other...We can disengage no concretely separable product of labor and capital” — Frank Taussig
The Firm as Nexus of Contracts

L: Armen Alchian (1914-2013)
R: Harold Demsetz (1930-2019)
"[A firm] is a team use of inputs and a centralized position of some party in the contractual arrangements of all other inputs. It is the centralized contractual agent in a team productive process," (p.778).
The Firm as Nexus of Contracts

L: Armen Alchian (1914-2013)
R: Harold Demsetz (1930-2019)
"Two men jointly lift heavy cargo into trucks. Solely by observing the total marginal productivity and making pay-weight loaded per day, it is impossible to determine each person's marginal productivity...In team production, marginal products of cooperative team members are not so directly and separably (i.e., cheaply) observable. What a team offers to the market can be taken as the marginal product of the team but not of the team members. The costs of metering or ascertaining the marginal products of the team's members is what calls forth new organizations and procedures," (pp.778).
Implications of Marginal Productivity Theory
Factor employment is determined by supply & demand of factor, where demand is driven by the factor’s marginal revenue product
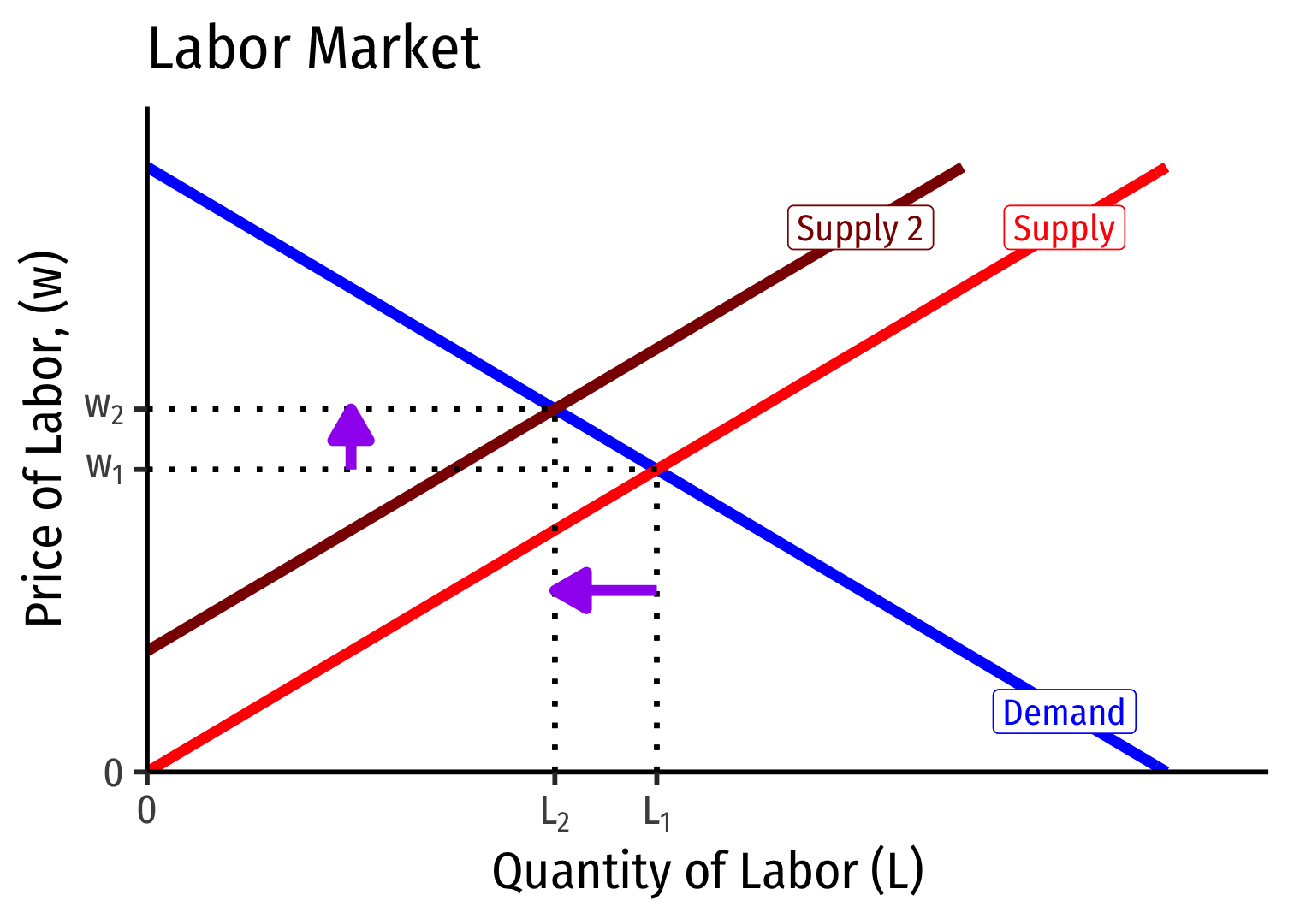
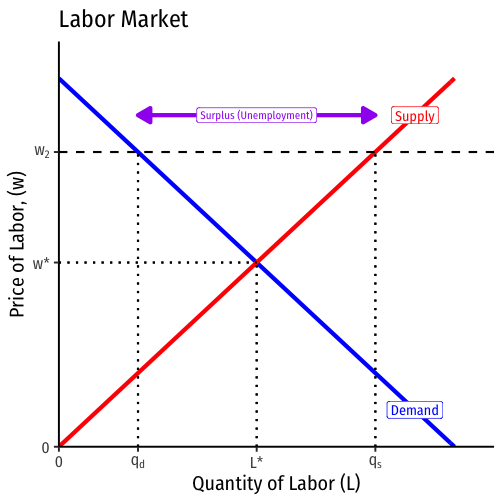
- if market price is above equilibrium (e.g. w2), a surplus (unemployment) of that factor
Prices will adjust downwards to equilibrium
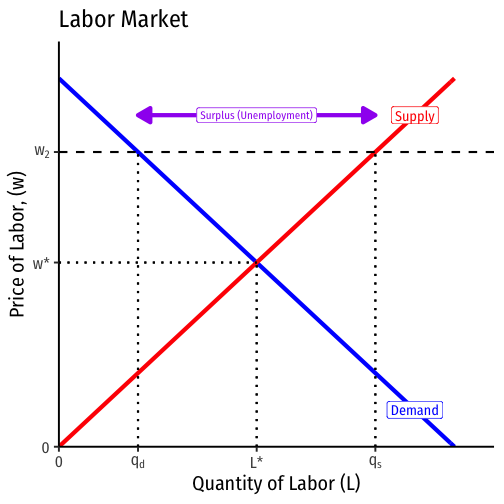
Implications of Marginal Productivity Theory
What implications does this have for macroeconomic policy?
Applied to the entire economy, implies that (non-frictional) unemployment is due to above-equilibrium factor prices
- markets will correct this by adjusting prices downwards
Anticipating Keynes:
- but is it that easy to lower wages??
- if workers have less income, will that affect aggregate demand?
Implications of Marginal Productivity Theory

John Bates Clark
1847—1938
MPT describes the outcome to which we are always approaching (i.e. perfect competition), it is an equilibrium state of rest
- actual prices in real world are not equilibrium prices, we are not in perfect competition
In long run equilibrium in perfect competition, factor prices are paid their marginal products
- p=MC, all factors are paid opportunity costs, firms break even and “exhaust the product” AR(q)=AC(q)
A scarce factor (talent, etc) will command higher prices (and reap economic rents), might be efficient, but is that moral?